Sudoku rule
Each row, col and 3 x 3 cell block must contain each of the numbers from 1 to 9.

Tip 1: Examine the influence of numbers to rows, columns and 3×3 cell blocks
What means influence? Remember the sudoku rule. It means in other words, that a number cannot be set on positions of a view (row, column or 3×3 cell block) that intersect with related views containing the number. The aim is, to find the one possible position for the number.
In this sudoku taken from the meSudoku app we examine the influence of the number 8 on a 3×3 cell block. We recognize, that only one position is possible for the number 8. Using this strategy consequently you can solve many sudokus.
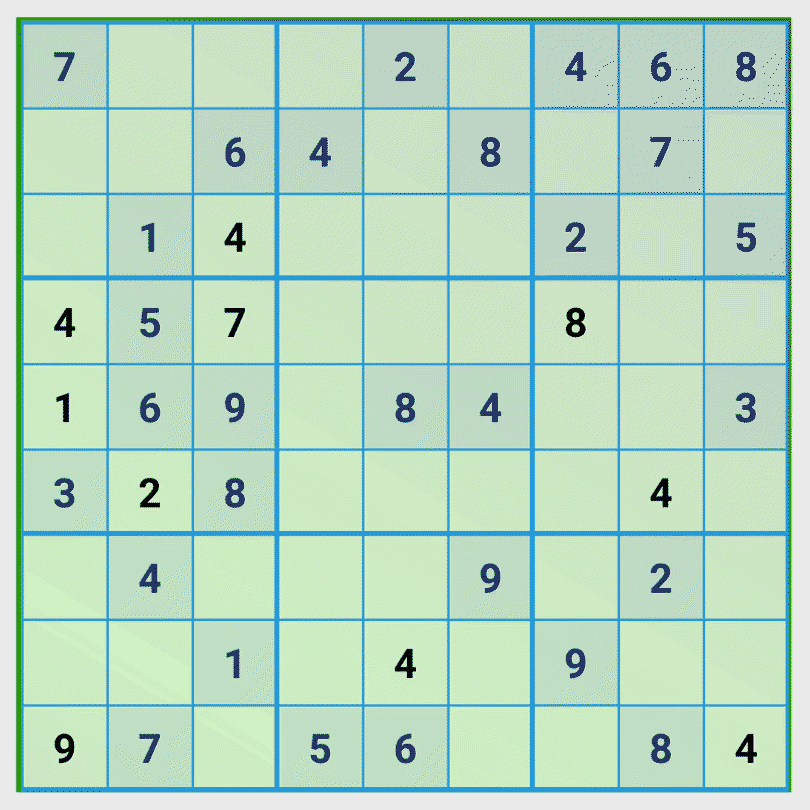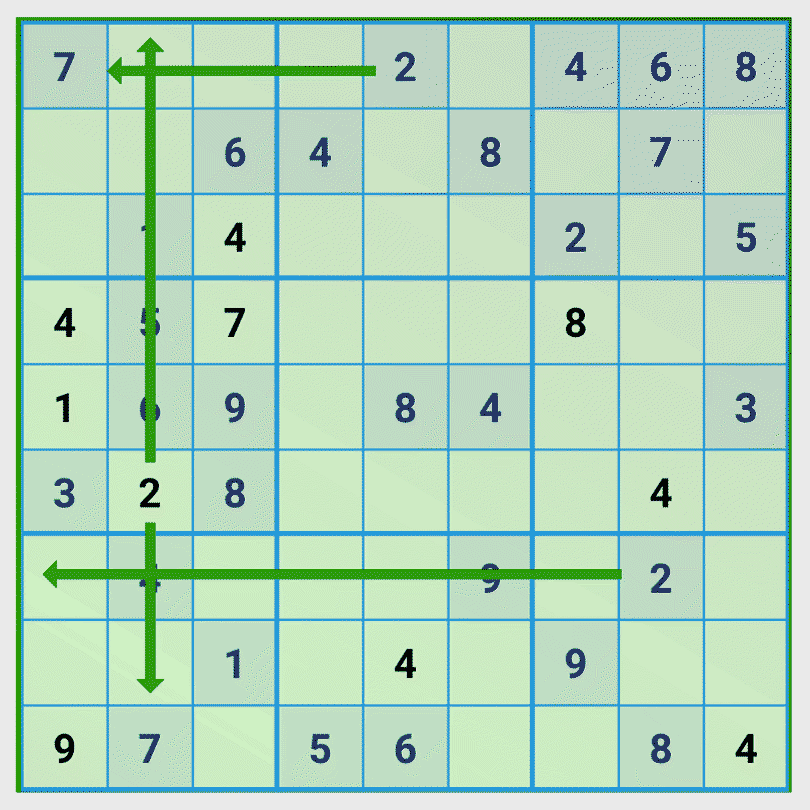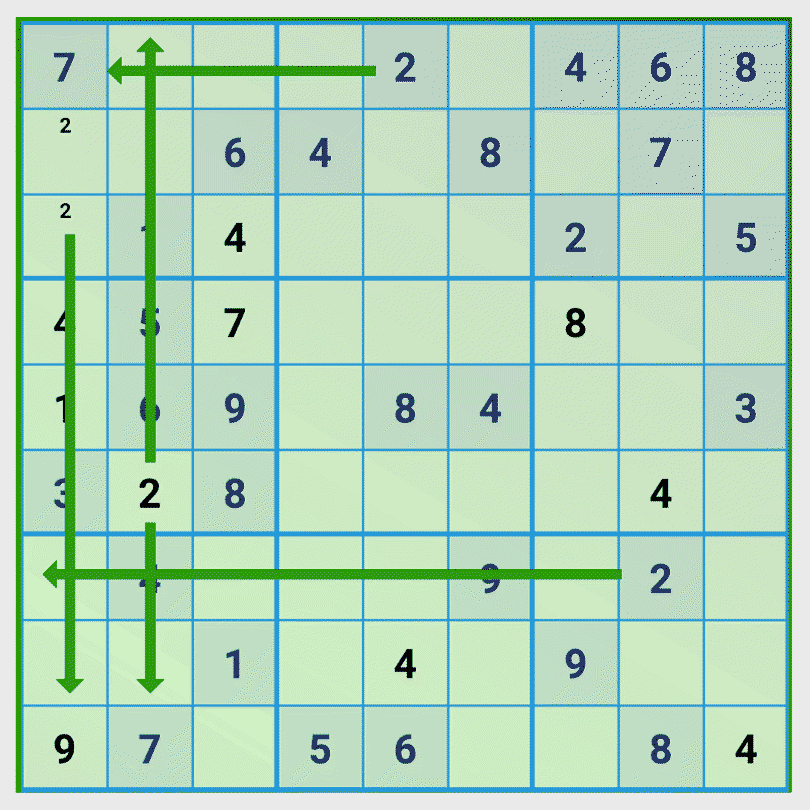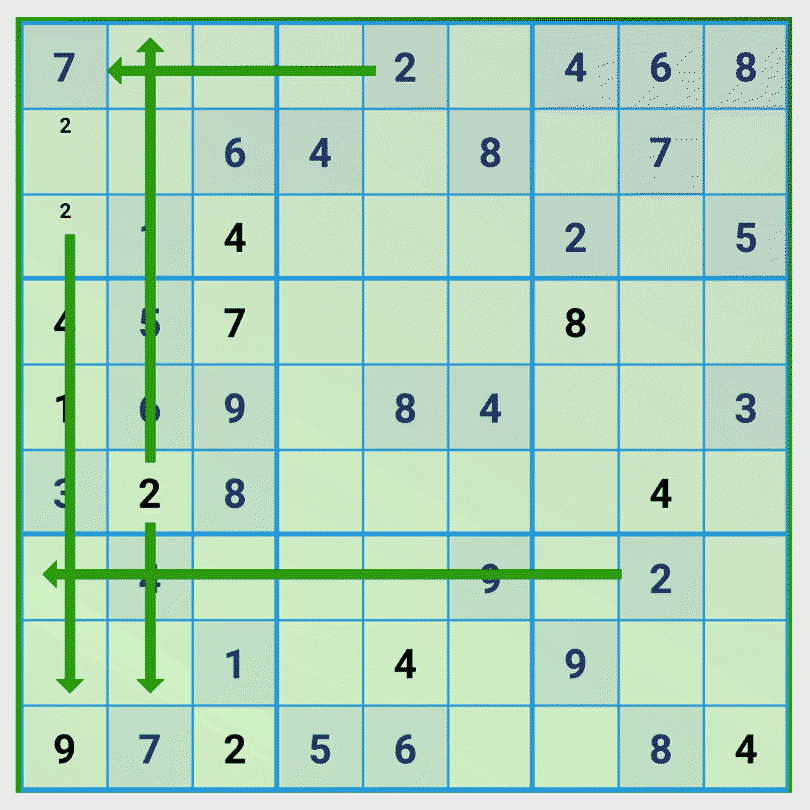
Tip 2: Optimize the examination the influence of numbers to rows, columns and 3×3 cell blocks
Using the strategy from Tip 1 we can see that the number 2 can only be in two positions in the first 3×3 block and that the two positions are in one column. So since the number 2 is in any case in this column, we can take this influence into account in our investigation.
Note: We did not have to use this technique in this game situation. The procedure described in tip 1 would have been sufficient if we had considered the influence of another number 2.
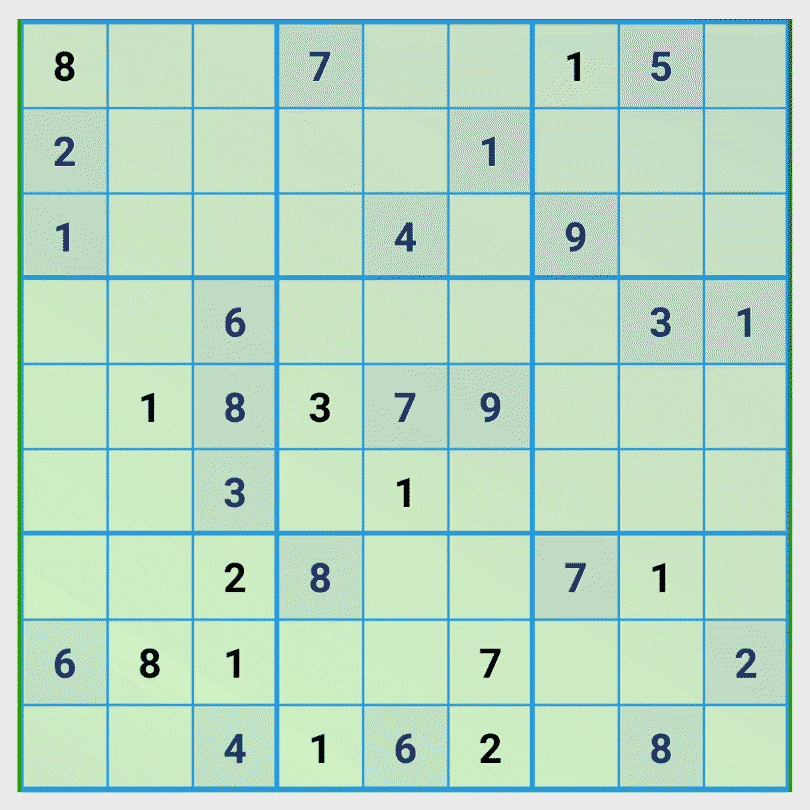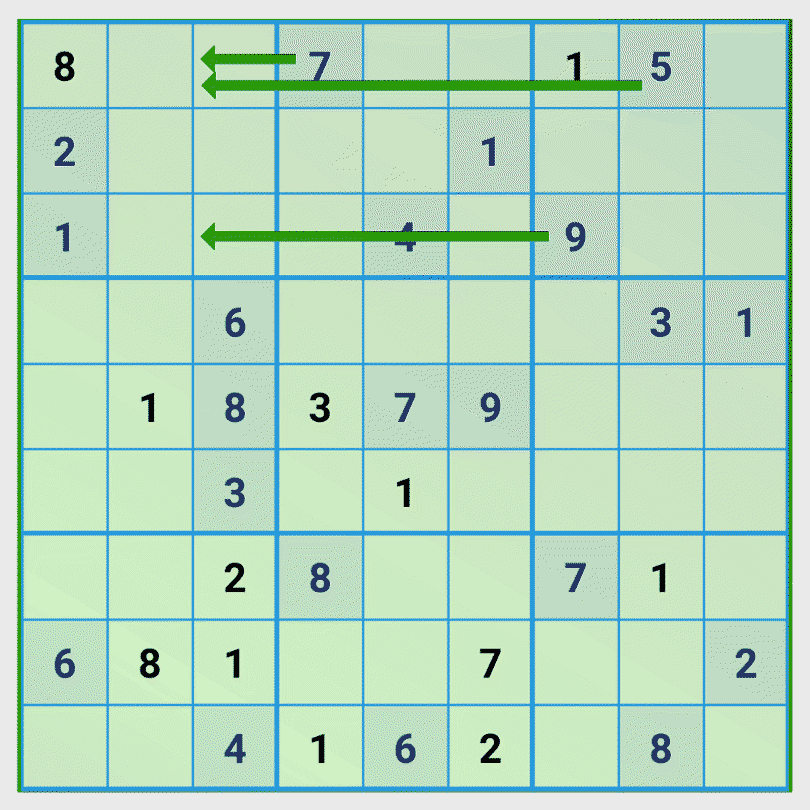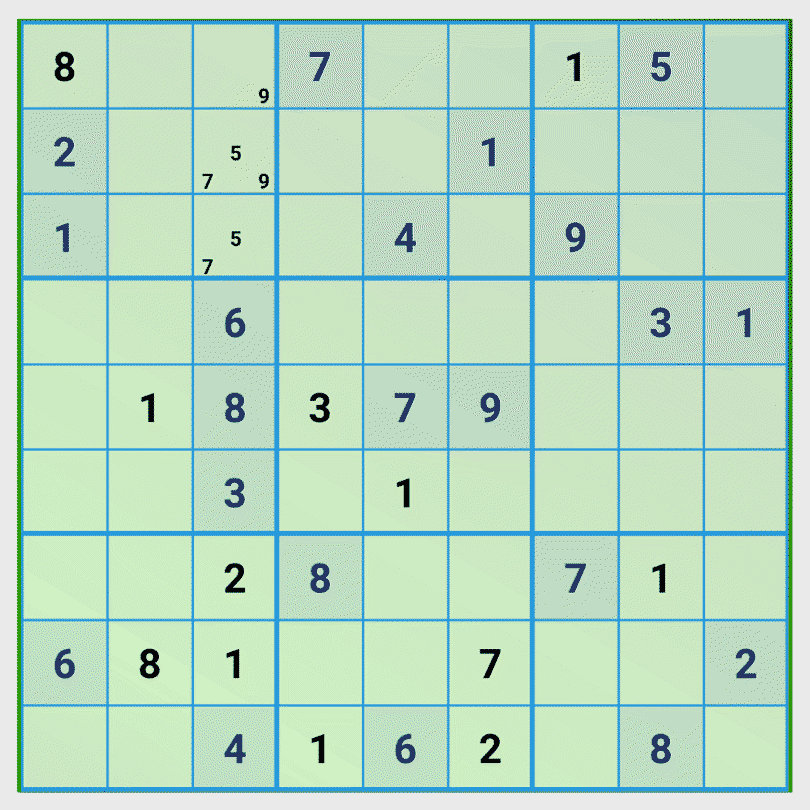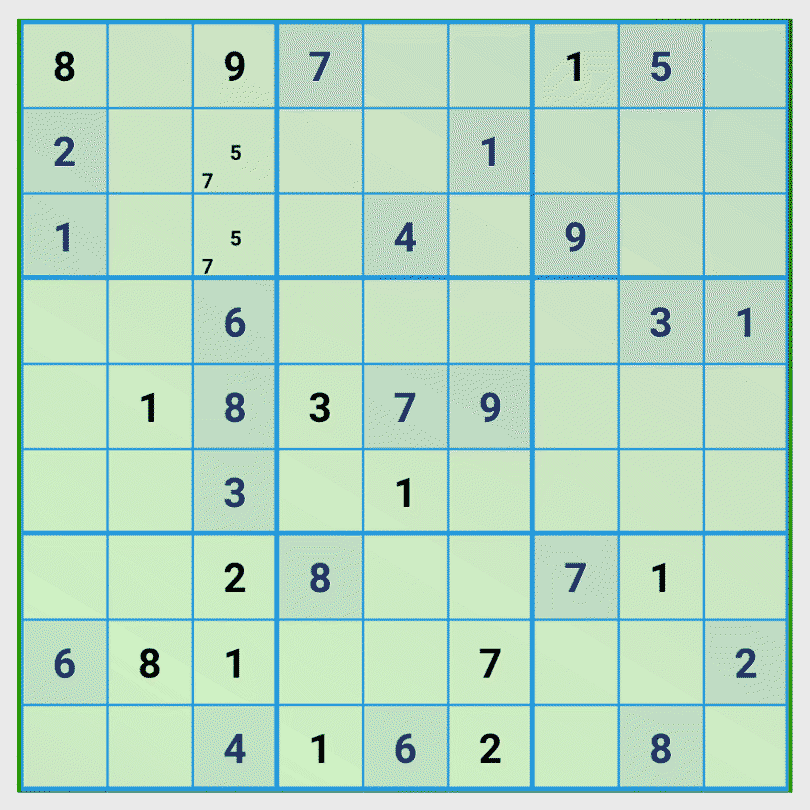
Tip 3: Calculate the missing numbers of an view and examine the influence of the related views
In this game situation we recognize that in column 3 the numbers 5, 7, 9 are missing. Then we examine the influence of the first three rows on the third column and recognize that only the number 9 can be set in the first field of the third column.
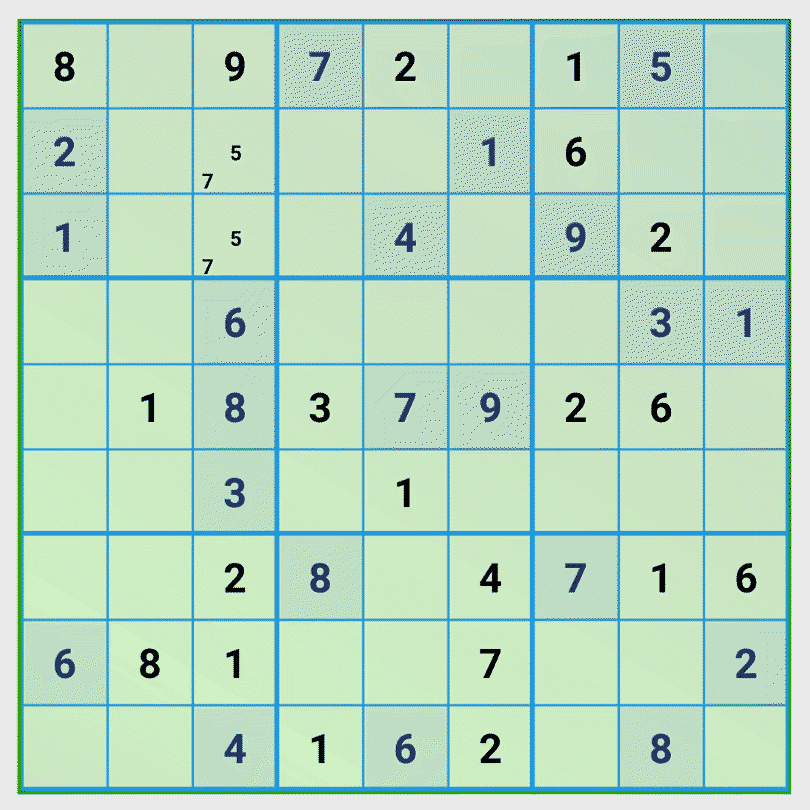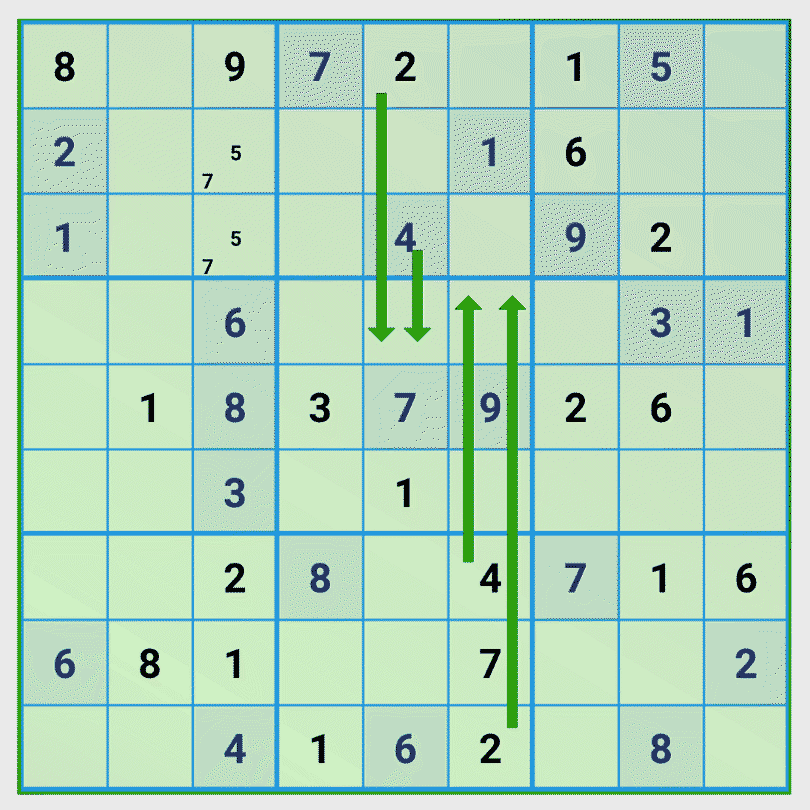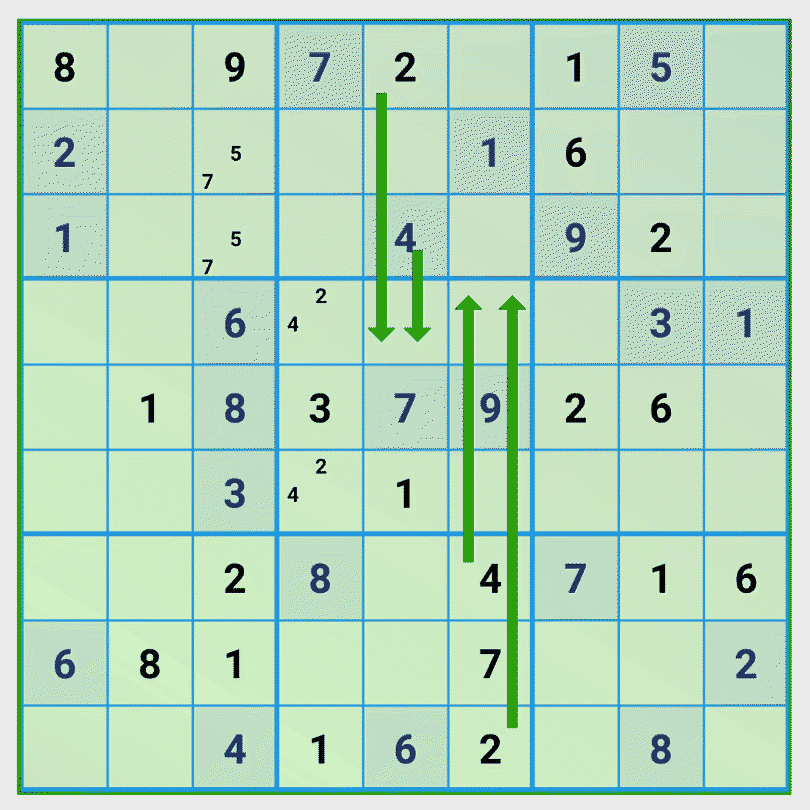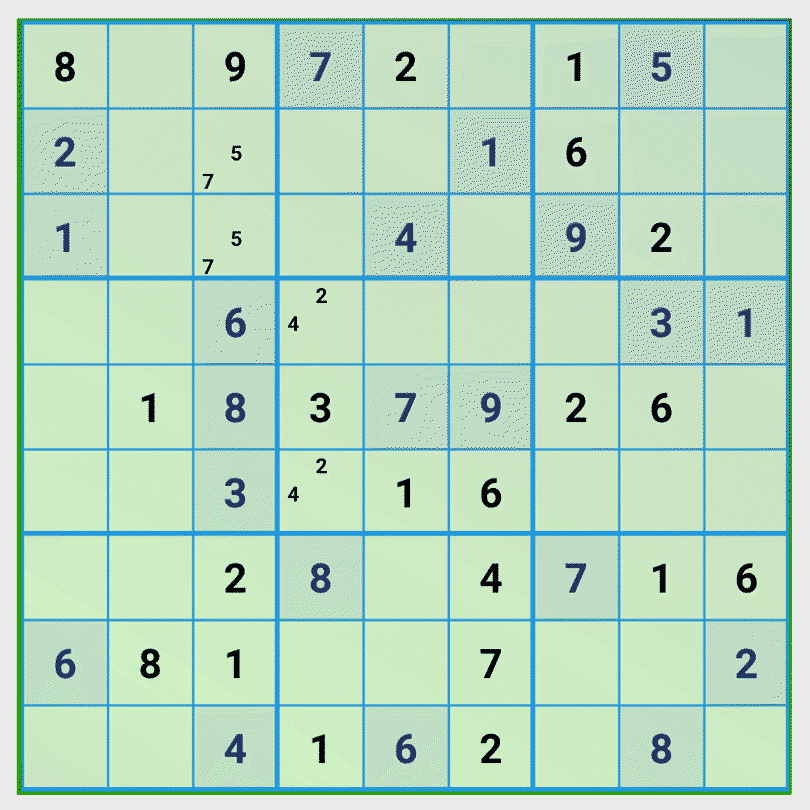
Tip 4: Find groups of digits that occupy fields according to the number of digits.
This tip is a variation of tip 2. We see that the numbers 2 and 4 of column 5 and 6 block the same 2 columns of the central 3×3 cell block and that the remaining column of the 3×3 block has exactly two empty fields. From this we conclude that in these two empty fields only the digits 2 and 4 can be correct and no other digits. Using now tip 1 brings the next number. Because two fields now are blocked, the projection of the number 6 of row 4 leads to one possible position for the number 6.
Tip 5: Forcing chains
The forcing chain is a method that perhaps helps to find a number in game situations where the methods described above fail. As the name suggest, we need to find chains composed of fields that have a relationship. A relationship exists between two fields if they are in the same row or column or 3×3 field block. Each field may only have 2 candidates. To link from one field to the successor, at least one candidate (chaining number) must be a candidate of the successor. The next link starts from the linked field and must use its other candidate (forced number) to link to the next field. A chain can be used as forcing chain if the last field forces a number in the first field of the chain. A forcing chain is closed if the last field forces the same number as the chaining number of the first field.
What can we conclude from this?
- If all the chains for both candidate numbers can be closed, the result is undefined.
- If you find for both candidate numbers at least one forcing chain that cannot be closed, you probably have an error in your candidate setting.
- If all the chains for one of both candidate numbers can be closed, but for the other number exists at least one chain, that cannot be closed, the searched number is the first one.

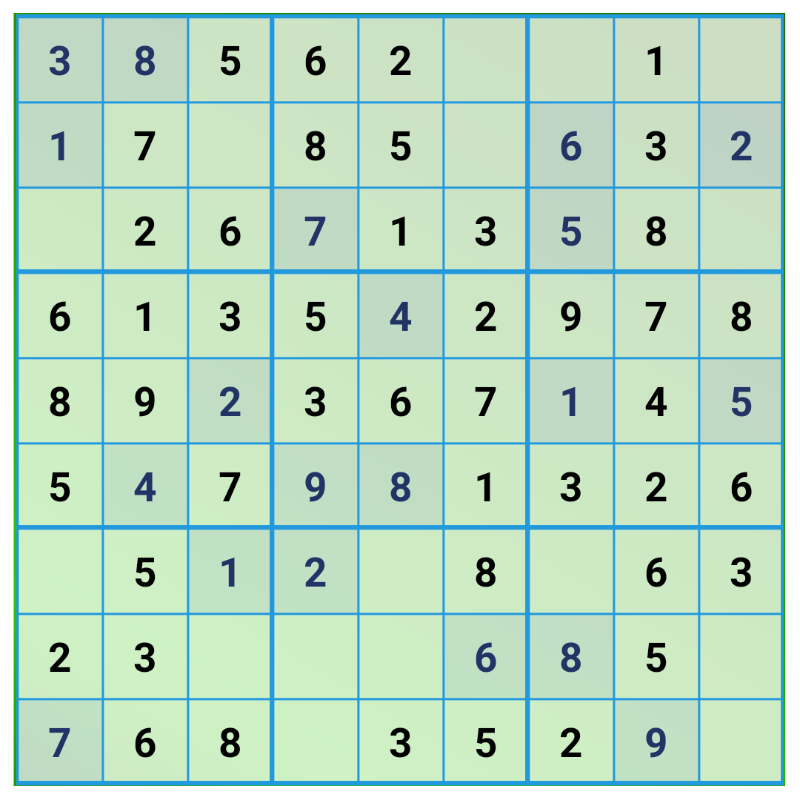
Step 1: Fill all fields with candidates
Enter the candidates in each field. Reduce them as much as possible. Use the tips 1 – 4 consequently.
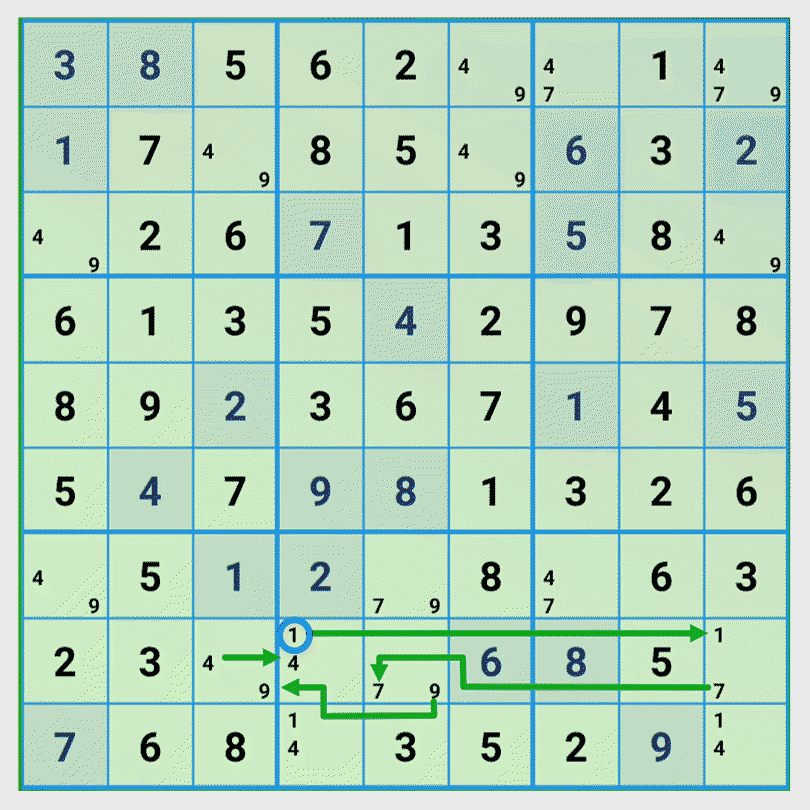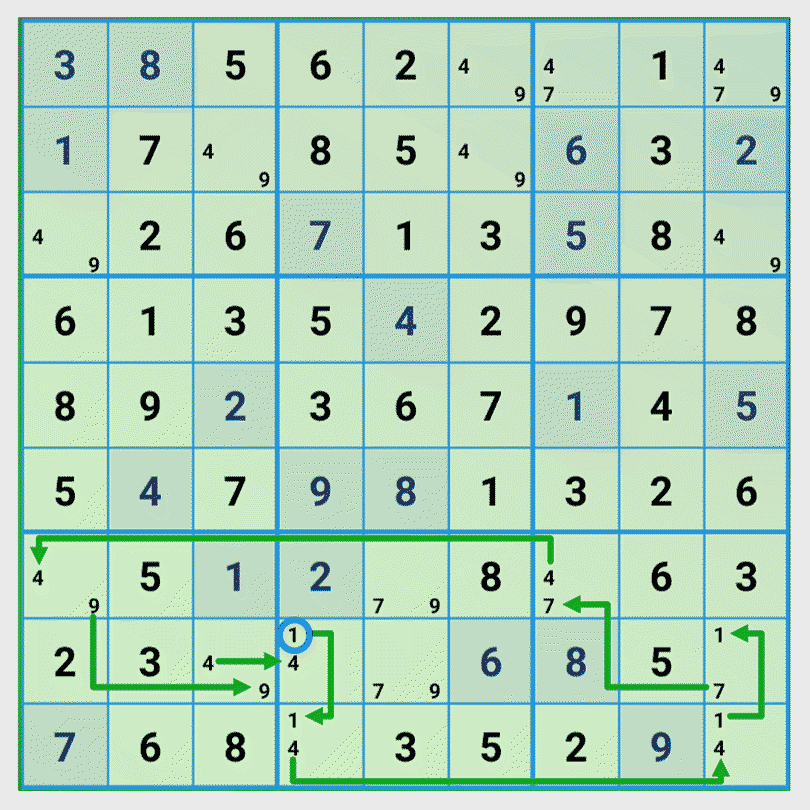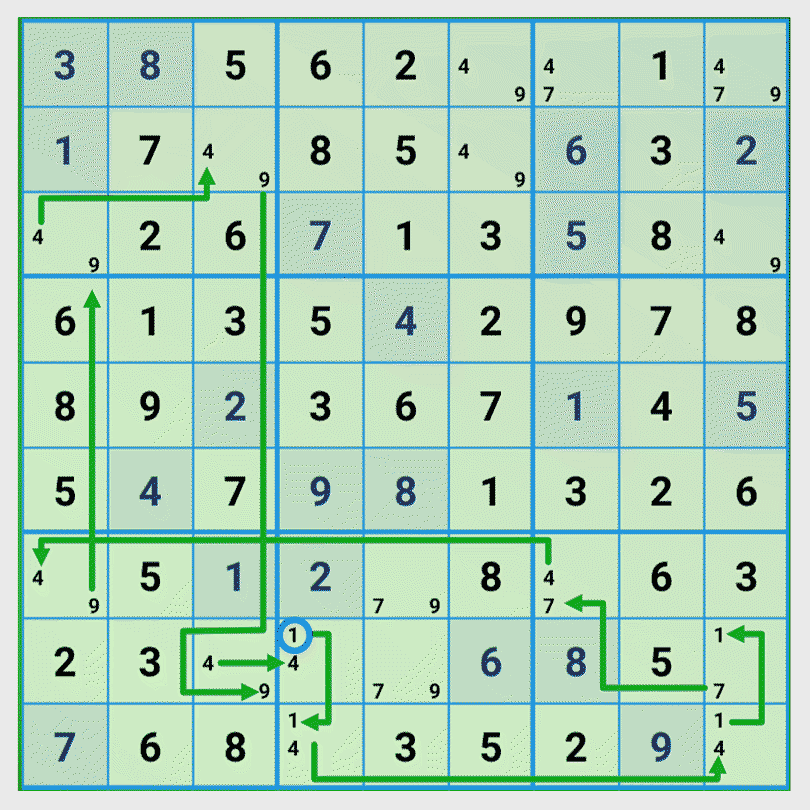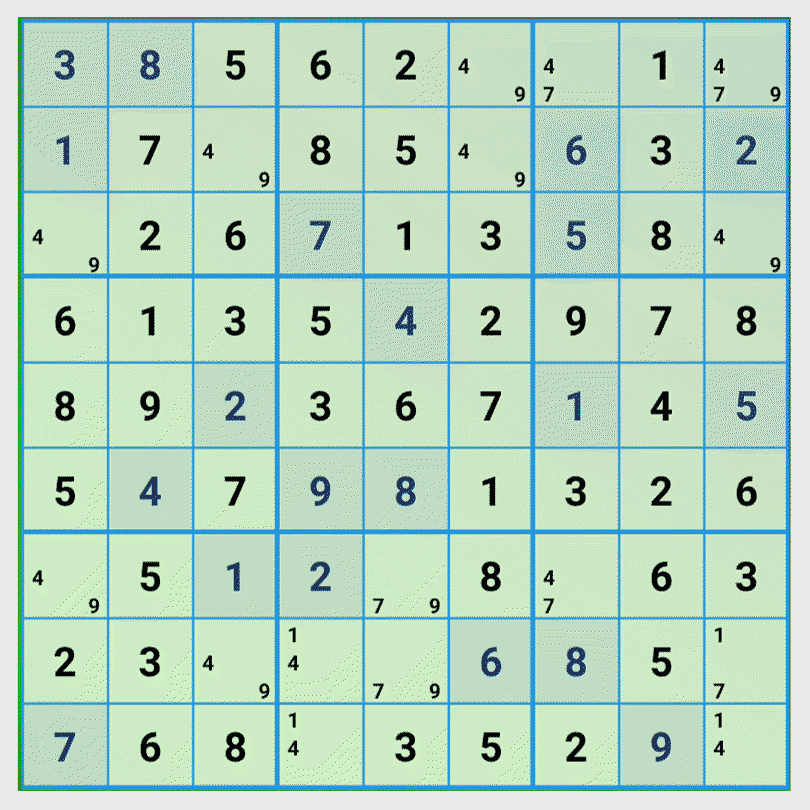
Step 2: Select a start field and a start value and find all possible chains
We select row 8 column 4 with the candidates {1, 4} and as start number the number 1.
| Link source | Link destination | ||||
|---|---|---|---|---|---|
| R | C | Chaining number | R | C | Forced number |
| 8 | 4 | 1 | 8 | 9 | 7 |
| 8 | 9 | 7 | 8 | 5 | 9 |
| 8 | 5 | 9 | 8 | 3 | 4 |
| 8 | 3 | 4 | 8 | 4 | 1 |
In the same manner, we find two more chains. All chains we found, lead to a valid solution: number 1. But that is not enough to put the number 1 in the field. We have to check the second number.
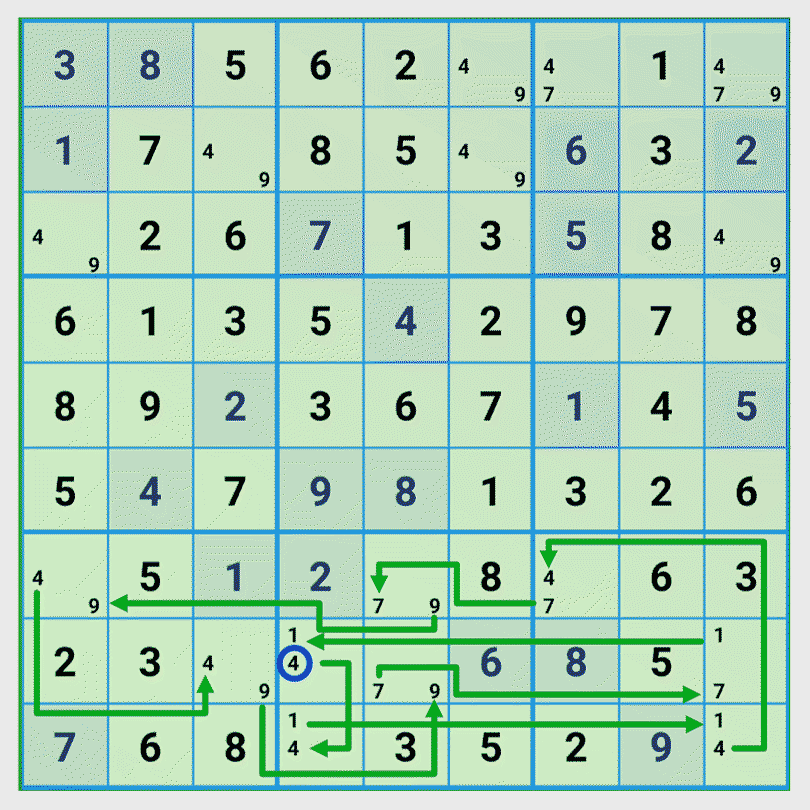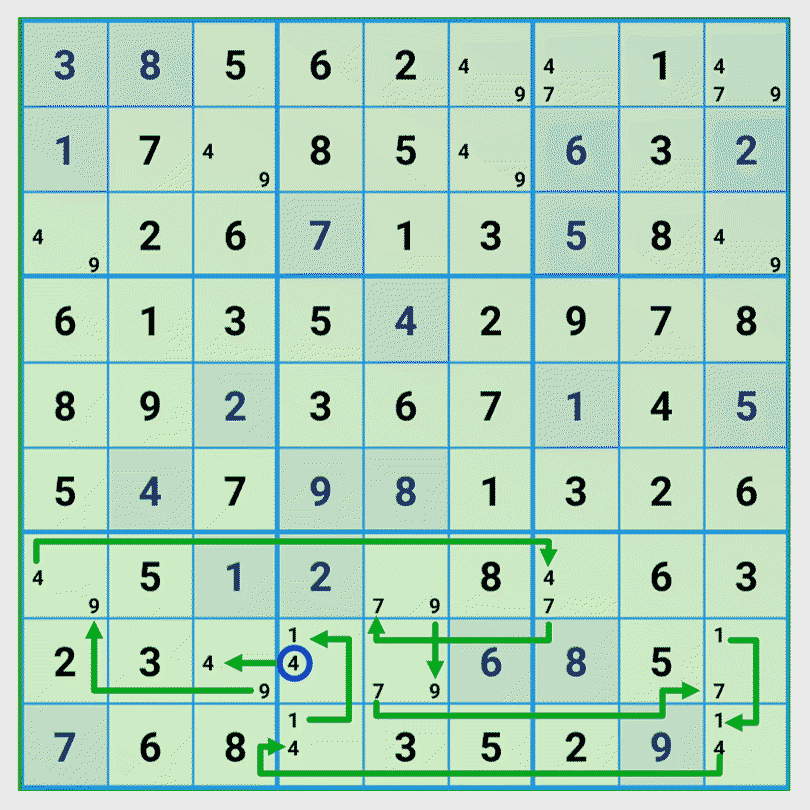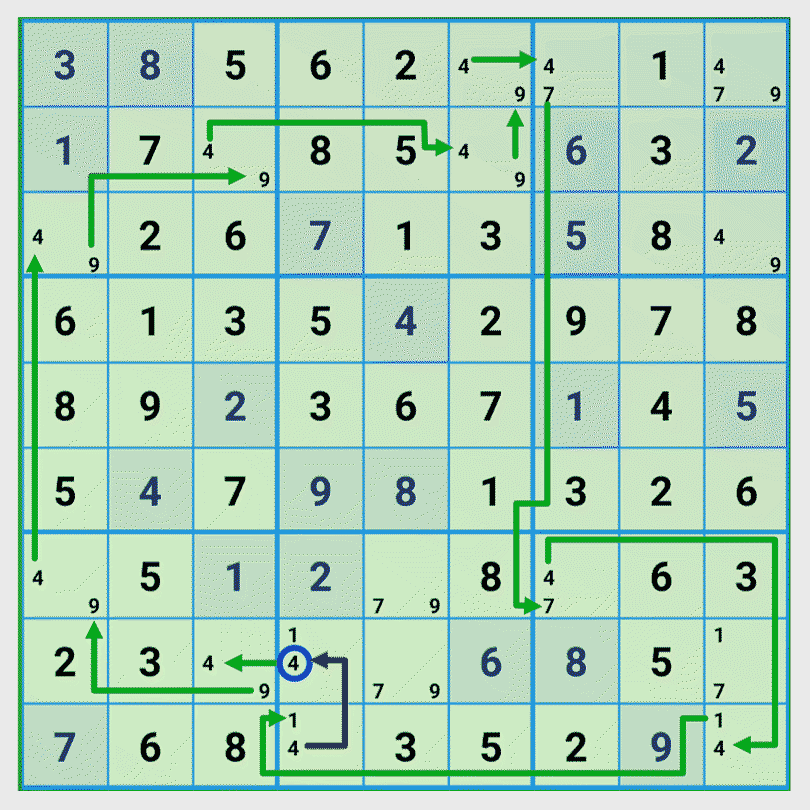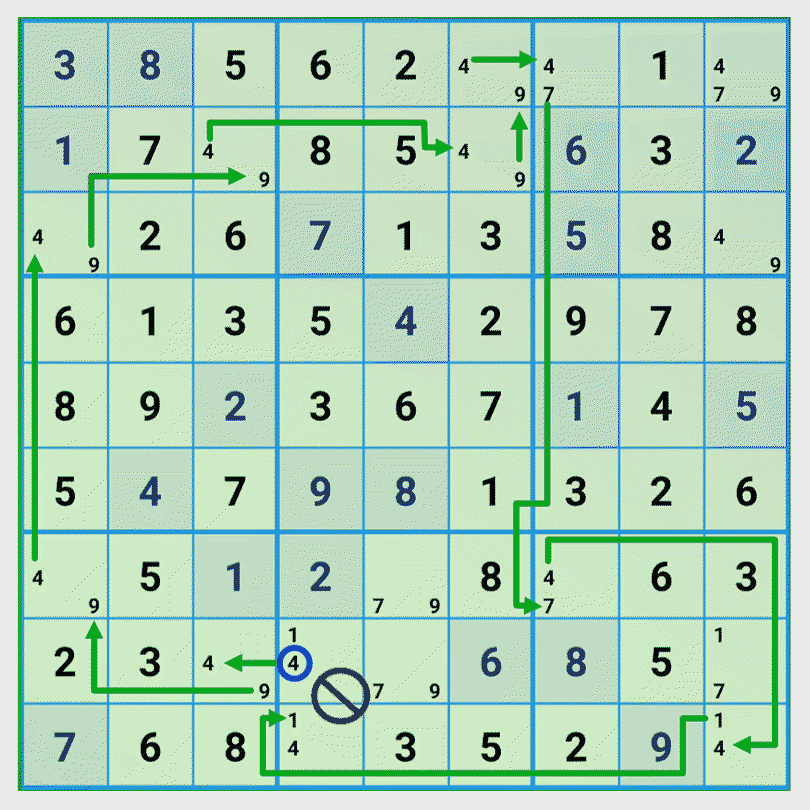
Step 3: Find all possible chains for the second number
We select row 8 column 4 with the candidates {1, 4} and as start number the number 4. We find two chains that lead to a valid solution and as third chain an invalid one. Let’s look at the invalid chain in detail.
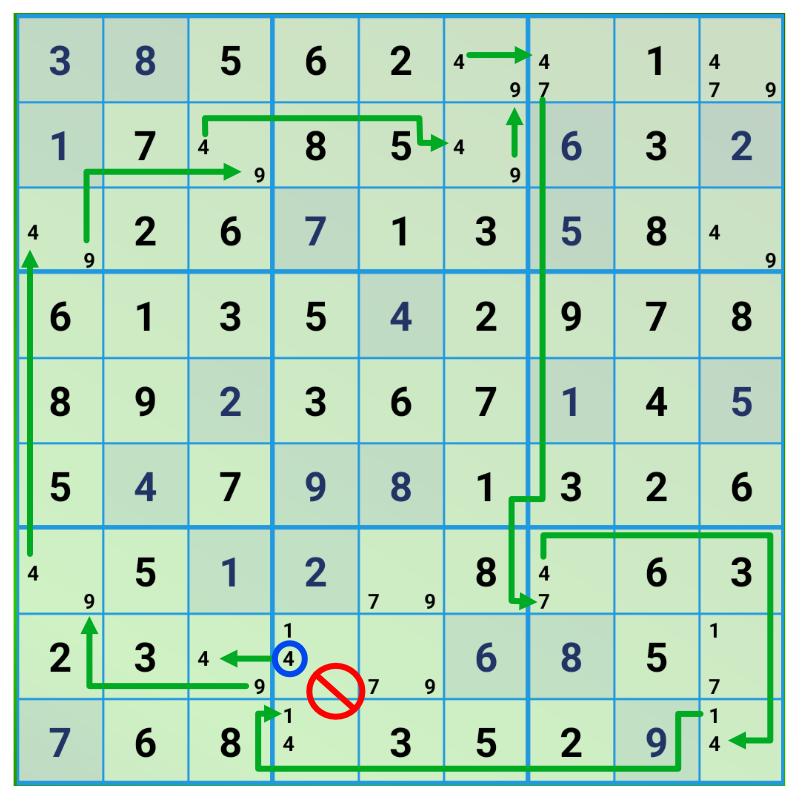
| Link source | Link destination | ||||
|---|---|---|---|---|---|
| R | C | Chaining num. | R | C | Forced num. |
| 8 | 4 | 4 | 8 | 3 | 9 |
| 8 | 3 | 9 | 7 | 1 | 4 |
| 7 | 1 | 4 | 3 | 1 | 9 |
| 3 | 1 | 9 | 2 | 3 | 4 |
| 2 | 3 | 4 | 2 | 6 | 9 |
| 2 | 6 | 9 | 1 | 6 | 4 |
| 1 | 6 | 4 | 1 | 7 | 7 |
| 1 | 7 | 7 | 7 | 7 | 4 |
| 7 | 7 | 4 | 9 | 9 | 1 |
| 9 | 9 | 1 | 9 | 4 | 4 |
| 9 | 4 | 4 | 8 | 4 | 1 |
The last link forces a number in the start field that doesn’t fit. The conclusion is that number 1 is the correct number.
